Upper Triangular Matrix Row Major Mapping

Back to: Data Structures and Algorithms Tutorials

Upper Triangular Matrix by Row-Major Mapping in C and C++:

In this article, I am going to discuss Upper Triangular Matrix by Row-Major Mapping in C and C++ Language with Examples. Please read our previous article, where we discussed Lower Triangular Matrix by Column Major Mapping in C and C++ Language with Examples.

Upper Triangular Matrix by Row-Major Mapping:

This is our upper triangular matrix. So non-zero elements are in the upper triangular part of this square matrix. a₁₂, a₁₃…, a₅₅ are non-zero elements. ‘i’ is the raw numbers and ‘j’ is the column numbers. But which elements are non-zero? We have a condition for finding non-zero and zero elements which is:

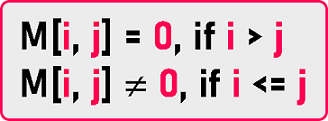
So, if i is less than or equal to j then the elements will be non-zero. If i is greater than J then the elements will be zero. Total number of non-zero elements is:

= 5 + 4 + 3 + 2 + 1, means,

= n + (n-1) + (n-2) + … + 3 + 2 + 1

= n * (n + 1) / 2.

Total number of zeros elements is:

= total no. of elements – no. of non-zero elements

= n² – n (n + 1) / 2

= n (n-1) / 2

This is how we can define our upper triangle matrix. Now how do we present this one in a single dimension array?

We will not be taking a two-dimensional array and filling it with these many zeros. We have to avoid storing zeros so that we can save space and processing time. So, what should be the size of the array? The size will depend on the number of non-zero elements. As we calculate no. of non-zero elements, so the size will be n * (n + 1) / 2. Let us create a single dimension array:

Here we have an array of the size 15 the indices start from 0 or 14 and we will map the above upper triangular matrix in this single dimension array. There are two methods for mapping the matrix:

1. Row Major
2. Column Major

Row Major mapping

Let’s see Row Major mapping:

Now we will map the matrix row by row in the single dimension array as:

1^st row:

2^nd row:

3^rd row:

4^th row:

5^th row:

In this way, all these elements will be mapped to this array. Now we need a formula so for formula let us take one example and observe it. As we already discussed formulas in the lower triangular matrix article, those formulas will be useful here. let us take one example and see.

We want to find the indices of M [4][5]. M [4][5] means the element which is present in the 4^th row and 5th column. As we can see in the array, M [4][5] is present on the 13^th index. The element is present in the 4^th row. So, we need to skip 1^st, 2^nd, and 3^rd row to reach on 4^th row.

1^st row having 5 elements: Index (M [4][5]) = 5 +

2^nd row having 4 elements: Index (M [4][5]) = 5 + 4

3^rd row having 3 elements: Index (M [4][5]) = 5 + 4 + 3

Now after skipping the 3 rows, we are on the beginning of 4^th row:

Now how much we should move ahead reach a₄₅? Just one element. So,

Index (M [4][5]) = [5 + 4 + 3] + 1

Index (M [4][5]) = 13

Here we got the 13^th index. This is looking similar to the column-major formula of the lower triangular matrix.

Index (M [4][5]) = [n + n-1 + n-2 + … + 3 + 2 + 1] + (j – i)

Index (M [4][5]) = [ (i-1) * n – (i-2)*(i-1) / 2] + (j – i)

This is the required formula for Row-Major Mapping of Upper Triangular Matrix. Now let see the code part:

Upper Triangular Matrix by Row-Major Mapping Code in C Language:

#include <stdio.h>
#include <stdlib.h>

struct Matrix
{
    int *B;
    int n;
};

void Set (struct Matrix *m, int i, int j, int y)
{
    if (i <= j)
        m->B[((i - 1) * m->n - (i - 2) * (i - 1) / 2) + (j - i)] = y;
}

int Get (struct Matrix m, int i, int j)
{
    if (i <= j)
        return m.B[((i - 1) * m.n - (i - 2) * (i - 1) / 2) + (j - i)];
    else
        return 0;
}

void Display (struct Matrix m)
{
    int i, j;
    printf ("\nMatrix is: \n");

    for (i = 1; i <= m.n; i++)
    {
        for (j = 1; j <= m.n; j++)
        {
           if (i <= j)
             printf ("%d ", m.B[((i - 1) * m.n - (i - 2) * (i - 1) / 2) + (j - i)]);
           else
             printf ("0 ");
        }
        printf ("\n");
    }
}

int main ()
{
    struct Matrix M;
    int i, j, y;

    printf ("Enter Dimension of Matrix: ");
    scanf ("%d", &M.n);
    M.B = (int *) malloc (M.n * (M.n + 1) / 2 * sizeof (int));

    printf ("Enter all the elements of the matrix:\n");
    for (i = 1; i <= M.n; i++)
    {
        for (j = 1; j <= M.n; j++)
        { 
           scanf ("%d", &y);
           Set (&M, i, j, y);
        }
    }
    Display (M);
}

Output:

Upper Triangular Matrix by Row-Major Mapping Code in C++ Language:

#include <iostream>
using namespace std;

class LowerTriangularMatrix
{
    private:
        int *B;
        int n;

    public:
        LowerTriangularMatrix ()
        {
            n = 3;
            B = new int[3 * (3 + 1) / 2];
        }

        LowerTriangularMatrix (int n)
        {
            this->n = n;
            B = new int[n * (n + 1) / 2];
        }

        ~LowerTriangularMatrix ()
        {
            delete[]B;
        }

        int GetDimension ()
        {
            return n;
        }

    void Set (int i, int j, int y);
    int Get (int i, int j);
    void Display ();
};

void LowerTriangularMatrix::Set (int i, int j, int y)
{
    if (i <= j)
        B[((i - 1) * n - (i - 2) * (i - 1) / 2) + (j - i)] = y;
}

int LowerTriangularMatrix::Get (int i, int j)
{
    if (i <= j)
        return B[((i - 1) * n - (i - 2) * (i - 1) / 2) + (j - i)];
    return 0;
}

void LowerTriangularMatrix::Display ()
{
    cout << "\nMatrix is: " << endl;

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
           if (i <= j)
             cout << B[((i - 1) * n - (i - 2) * (i - 1) / 2) + (j - i)] << " ";
           else
             cout << "0 ";
        }
        cout << endl;
    }
}

int main ()
{
    int d;
    cout << "Enter Dimensions: ";
    cin >> d;

    LowerTriangularMatrix lm (d);

    int x;
    cout << "Enter All Elements: " << endl;
    for (int i = 1; i <= d; i++)
    {
        for (int j = 1; j <= d; j++)
        { 
            cin >> x;
            lm.Set (i, j, x);
        }
    }

    lm.Display ();
    return 0;
}

Output:

In the next article, I am going to discuss Upper Triangular Matrix Column Major Mapping in C and C++ Language with Examples. Here, in this article, I try to explain Upper Triangular Matrix Row Major Mapping in C and C++ Language with Examples and I hope you enjoy this Upper Triangular Matrix Row Major Mapping in C and C++ Language with Examples article.