Binary Trees in Data Structure

Back to: Data Structures and Algorithms Tutorials

Introduction to Binary Tree in Data Structure:

In this article, we will discuss Binary Tree Data Structure in more detail. Please read our previous article, which briefly introduces the Tree Data Structure. First, Let us explore how to calculate the number of binary trees that can be formed for a given set of nodes.

What is a Binary Tree?

A Binary Tree is a hierarchical data structure in which each node has at most two children, referred to as the left and right children. It’s a specialized form of tree in which every node can have zero, one, or two children. Binary trees are commonly used in computer science for various applications such as searching, sorting, and hierarchical data representation.

• Root: The topmost node in the tree.
• Nodes: Each node in the tree contains a value and references to its children.
• Leaves: Nodes with no children.
• Subtrees: Trees formed by each child node and its descendants.

How do we calculate the number of binary trees generated for a given set of nodes?

If the number of nodes is given, how many different binary trees of various structures can be generated? There are two types of nodes:

1. Unlabelled Nodes
2. Labeled Nodes

Let us start with unlabelled nodes.

What are Unlabelled Nodes in a Binary Tree?

Unlabelled Nodes in a binary tree are nodes that do not have unique identifiers or labels. The focus is on the tree’s structure rather than its values. In this context, two binary trees are considered the same if they have the same structure, regardless of the values or labels on the nodes.

There are three empty nodes. Labeling is absent, i.e., nothing is written on these nodes (1, 2, 3, or A, B, C). These are unlabelled nodes. So, if three nodes are given, how many different binary trees can be generated? Let us first draw all the possible different structures.

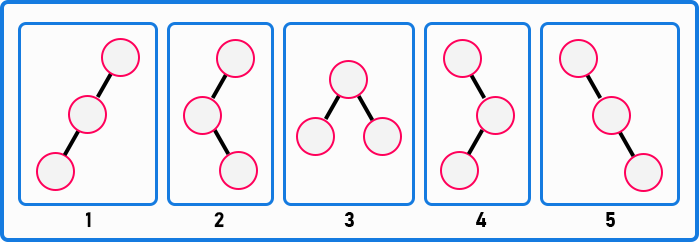
We can generate five differently shaped binary trees when given three unlabelled nodes.

T (3) = 5

Here, T is the function, 3 is the number of nodes, and 5 is the number of different binary trees. Let’s see how many binary trees can be generated if four unlabelled nodes are given.

Now, let us draw all possible binary trees.

As you can see, we first drew seven different binary trees and then their mirror images. Thus, we have drawn 14 different binary tree shapes for four unlabelled nodes.

T (4) = 14

So, if the number of nodes is 4, we will have 14 differently-shaped binary trees. We drew the binary trees for three and four nodes. Do we need to draw them every time to check how many differently shaped binary trees can be formed? No. We drew them to explain to you. There is a formula by which we can determine the total number of differently shaped binary trees based on the number of nodes. The formula is:

Catalan Number: T (n) = ²ⁿC_n / (n + 1)

This is a famous formula known as the Catalan Number. If the ‘n’ number of nodes is given, this formula will provide the total number of binary trees that can be generated. Let us calculate how many binary trees can be generated if five unlabelled nodes are given.

T (5) = ^{2 * 5} C ₅ / (5 + 1)

T (5) = ¹⁰ C ₅ / 6

T (5) = (10 * 9 * 8 * 7 * 6) / (5 * 4 * 3 * 2 * 1) * 6

T (5) = 42

So, 42 differently shaped binary trees can be generated when five unlabelled nodes are given. We can find the total number of 42 differently-shaped binary trees for any given number of nodes. Drawing all 42 shapes is not practical.

Height of Binary Tree:

Here, we need to observe one thing: what could be the maximum height of a binary tree when three nodes are given? Height starts from 0 onwards, so 0, 1, then 2. Thus, the maximum height can be 2 when three nodes are given.

In this diagram, the 1st, 2nd, 4th, and 5th shapes of binary trees have a maximum height of 2, but the 3rd shape has a height of 1. So, the number of trees with maximum height is 4.

N = 3, number of trees with max height = 4 = 2²

If four nodes are given, the maximum height of a binary tree can be 3. You can refer to the above diagram, where we showed you all the shapes of binary trees with four nodes. In that diagram, eight trees have the maximum height.

N = 4, number of trees with max height = 8 = 2³

Now, for n = 5, how many trees will have the maximum height?

N = 5, number of trees with max height = 16 = 2⁴

Sixteen trees can be generated with maximum height when the number of nodes is five. Now, we can generalize the formula for any number of nodes as,

Total Number of trees with max height when there are ‘n’ nodes = 2^{n – 1}

With this formula, we can determine the total number of binary trees with maximum height that can be generated for a given number of nodes.

Now, let us derive another formula for the Catalan Number. We will write a few values obtained from the Catalan number and see how to develop another formula.

How do we derive another formula using the Catalan Number?

Let us first create a table of values for the Catalan Number.

We will calculate the Catalan Number for a few nodes and write the results in this table. For n = 0, we will get 1 from the Catalan Number.

For n = 1, we will still get 1 from the Catalan Number.

For n = 2, we will get 2 from the Catalan Number.

For n = 3, we’ve already calculated the value that is 5.

For n = 4, we’ve already calculated the value that is 14.

For n = 5, we will get 42 from the Catalan Number.

Now, we will find the value for n = 6 using a different method other than this formula:

T (6) = (1 * 42) + (1 * 14) + (2 * 5) + (5 * 2) + (14 * 1) + (42 * 1)

This will give the value for n = 6. Now, how are we multiplying these values? Are we randomly multiplying them? No. Let’s understand how the values are multiplied.

Observe the above diagram. By observing the table and multiplications, you can easily understand how to multiply the values to get the value for n = 6. If it is still unclear, let’s look at the image below.

This diagram shows how the multiplication was done to get the value for n = 6. We hope it’s clear to you now.

T (6) = (1 * 42) + (1 * 14) + (2 * 5) + (5 * 2) + (14 * 1) + (42 * 1)

T (6) = 132

Here, we got the Catalan value for n = 6 with another approach. Now, let us use the Catalan Number to check whether we got the right value.

T (n) = ²ⁿ C _n / (n + 1)

T (6) = ^{2 * 6} C ₆ / (6 + 1)

T (6) = ¹² C ₆ / 7

T (6) = (12 * 11 * 10 * 9 * 8 * 7) / (6 * 5 * 4 * 3 * 2 * 1) * 7

T (6) = 132

So, both methods give us the same value, meaning the method provides the correct value for any number of nodes. Now, for the above method, where we multiply the values of n, let us prepare a general formula.

T (6) = (1 * 42) + (1 * 14) + (2 * 5) + (5 * 2) + (14 * 1) + (42 * 1)

This is the expression for n = 6.

T (6) = (T₀ * T₅) + (T₁ * T₄) + (T₂ * T₃) + (T₃ * T₂) + (T₄ * T₁) + (T₅ * T₀)

Here, T denotes the Catalan Number for a particular number of nodes. Now, let us write the generic version of the above expression.

Here, we got the general formula. You may be wondering where the (i – 1) & (n – i) terms come from. Let us explain this with the help of a diagram.

If you look at the highlighted numbers in the above image, you will find that they are increasing from start to end. We’ve taken T (i—1) in the formula because the starting number is 0.

The highlighted numbers in this image decrease from the beginning to the end of the expression. That’s why we’ve taken T (n—i) in the formula. Now, we have two formulas.

We can also write the Catalan Formula in this form. The first is the combination formula, and the second is the recursive formula. That’s all about the formulas. Now, let us learn about labeled nodes.

What are Labelled Nodes in a Binary Tree?

Labeled nodes in a binary tree refer to nodes that have unique identifiers or labels. Each node in the tree is distinguishable from the others based on its label, even if the tree structure is the same. The number of distinct binary trees increases when nodes are labeled because the identity of each node matters, leading to different possible configurations.

The nodes on which something is written, i.e., any alphabet, digits, etc. In the above example, A, B, and C are labels. So, how many binary trees can be generated if labeled nodes are given? As we know, we can generate five trees with unlabelled nodes. The formula for the total number of binary trees is the Catalan Number or the one we derived above.

In unlabelled nodes, we can generate five trees with three nodes. However, in labeled nodes, a tree structure can have multiple forms when we change the position of the labels. Let’s understand this with an example.

This is one of the possible binary tree structures when three labeled nodes are given. How many ways can we arrange the three labels in this structure? Labels can be arranged in 3 factorial ways, which is 6 (3! = 3 * 2 * 1).

These are the ways we can arrange the labels. The shape remains the same, but we change the labels’ position, so the labels’ permutation changes. There are six ways in which we can arrange the nodes’ labels: ABC, ACB, BCA, BAC, CAB, and CBA. Thus, one shape can be filled in 3! ways.

The above diagram is an example of unlabeled nodes. In labeled nodes, each shape of unlabeled nodes can be filled in 3! ways. So, how many such shapes can be generated for labeled nodes?

Total number of binary trees (where label nodes are 3) = 5 * 3! = 30

Here, 5 is the total number of unlabeled shapes, and 3! represents the different arrangements of labels in a particular shape. Therefore, 30 binary trees can be generated when three labeled nodes are given.

For n label nodes, the Total number of binary trees (where label nodes are n) = s * n!

Here, s is the total number of possible shapes, and n! is the number of arrangements of labels in a particular shape. The formula is:

T (n) = (²ⁿC_n / (n + 1)) * n!

In this formula, n! represents the arrangement of labels. If you look at the formula and separate it into two parts, the combination part is for shapes and n! is for the arrangement of labels. The combination part gives you the total number of different shapes, and n! gives you the number of ways to arrange the labels in one shape. 

In the next article, I will discuss Height vs. Nodes in a Binary Tree with Examples. In this article, I explain Binary Tree Data Structure in C Language with Examples. I hope you enjoy this article on Binary Tree Data Structure in C Language.