Stack Operation using Array

Back to: Data Structures and Algorithms Tutorials

Stack Operation using Array:

In this article, I will discuss how to Perform Operations on a Stack using an Array. Please read our previous article discussing Stack Implementation using Array. 

Stack Push() Operation:

This operation inserts an element into the stack. Let’s see how to insert an element into the stack using an array.

Initially, the Top pointer is pointing at -1, indicating that there are no elements in the stack. To push a value, such as 8, we have to increment the Top pointer by 1 (Top++) and insert 8 where the Top is pointing.

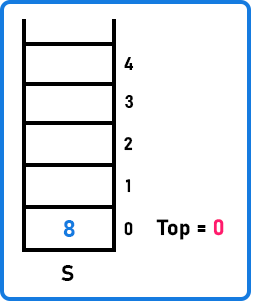
Next, we will insert another value, let’s say 12. To do this, we have to first increment the Top by 1 and then insert 12 at the index indicated by the Top.

Let’s insert a few more values.

The top currently points to index 3. To insert another value, such as 25, we have to increment the Top pointer by 1 and insert 25 at the index indicated by the Top.

Now, can we insert another value? We cannot do so because there is no available free space. The top is currently at index 4, which is equal to the Array size minus 1. This indicates that the stack is full (Top == size-1). So, before insertion, we must check whether the stack is full or not. If it is full, we can’t insert more elements, and if it is not full, we will increment the top pointer and then insert the element. So, this is the procedure for insertion. Now, let us write a function for insertion.

Stack Push() Function

We will write a function push(). It will take two parameters: the stack in which we want to insert an element and the element that we want to insert.

void push (Stack *st, int x){
    if (st->Top == st->size-1)
        printf("Stack Overflow");
    else{
        st->Top++;
        st->S[st->Top] = x;
    }
}

To modify the stack (insertion or deletion), we need to use call by address or call by reference. Therefore, we will take the pointer *st of the Stack structure. As we are modifying the stack and not returning anything from the function, we will use the return type void.

Inside the push function, we first need to check the stack full condition, i.e., Top == size-1. If this is the case, we’ll print “Stack Overflow.” We access the Top and size data members with the Stack object using the arrow symbol, which is used when working with pointers. In the else part, we will insert the value into the stack. For insertion, we have seen that first, the top pointer will be incremented, and then the value will be inserted. Therefore, we follow the same procedure. Now, let us look at the next operation, which is a deletion or pop function.

Stack Pop() Operation:

Here, the Top is pointing at 25 (index 4), so if we want to pop out a value, we need to retrieve the value at the top and then decrement the top pointer.

So, the value 25 is deleted from the stack. Let’s remove 19 from the stack.

So, the value 19 is deleted from the stack. If we keep deleting till the last element of the stack,

Here, 8 is the last element. If we also delete this, then,

As the last element is deleted, the Top becomes -1. Can we delete any more values? No, because there are no values. How do we know there are no values? Because the stack is empty, and ‘Top’ points at -1. Therefore, ‘Top == -1’ is the condition for an empty stack. So, before deletion, we should confirm whether there are any elements present in the stack or not.

In our pop function, we will print the message ‘Stack Underflow’ if the user tries to delete elements when ‘Top’ becomes -1. Now, let us write a function to delete the values from the stack.

int pop (Stack *st){
    int x = -1;
    if (st->Top == -1)
        printf("Stack Underflow");
    else{
        x = st->S[st->Top];
        st->Top--;
    }
    return x;
}

This is our pop function. Let us explain it briefly.

So again, we have used call by reference because we want to modify the same stack that is passed as a parameter in the pop function. Therefore, we have taken the *st pointer. By using the pointer, we can access all the members of the Stack structure, i.e., size and top. As we want to notify the user that the given value has been deleted, this function has to return that deleted value. So, the return type should be the type of values present in the stack (in our case, int).

The first condition of the pop function will check whether we can delete a value or not. It checks for underflow (Top == -1). If ‘Top’ is not -1, S[Top] will be stored in x, and the ‘Top’ pointer will be decremented by one. At the end, the deleted value that is stored in x will be returned by the function. We have initialized x with -1 because if nothing is deleted in the stack, then -1 will be returned. If this function returns -1, it means the stack is empty.

So that’s all about push and pop functions. Now, one important thing that we have to discuss is the time taken for pushing an element. Just incrementing the top pointer and inserting a value, so the time was constant. Similarly, what time was taken to delete an element? Just take out the value and decrement the top pointer. So here also, time is constant. So, the time taken by push and pop operations is constant. Now, let us look at the peek operation.

Stack Peek() Operation:

This function will find the element at the given position. Inside the stack,

The last element of the array is said to be the first element of the stack. So, here, 19 is the first element of the stack. If we give position 2, we will get element 14, and for position 3, we will get 12, and so on. Actually, in an array, the indices are moving up from 0, but the position in the stack means we have to start from the end of the array. So, we need a formula to map this relationship. Let’s take some examples and study how we can build up a formula for this.

Case 1:

If we say position 1, the index for that position will be 3.

Case 2:

If we say position 2, the index will be 2.

Case 3:

If we say position 3, the index will be 1.

Case 4:

If we say position 4, the index will be 0.

The top pointer will help us obtain indices. For position 1, we want index 3. See if the Top is 3 for this case. For position 1, if we subtract 1 from the Top pointer and then add 1, i.e., 3−1+1=3. Let’s check this formula with other positions.

• For position 2, if we subtract 2 from the Top pointer and add 1, i.e., 3−2+1=2. So, the index is 2.
• For position 3, if we subtract 3 from the Top pointer and add 1, i.e., 3−3+1=1. So, the index is 1.
• For position 4, if we subtract 4 from the Top pointer and add 1, i.e., 3−4+1=0. So, the index is 0.

This formula works for all the cases that we listed above. So, with the help of the Top pointer, we can get the index in an array.

The formula for obtaining the index is,

Index = Top – Position + 1

So, this is all you have in the formula from observations. We obtained this formula by observing the positions and Top pointer. By using this formula, we can convert the position into an index in an array. Let us use this formula and write the peek function.

The peek function will take two parameters, position and the stack. Should it be with call by reference or call by value? Call by value is enough because we are just reading the contents of the stack here, and we don’t want to modify it. The position parameter will be an integer. As the peek function returns the position (an int value), it should be of type integer. Now, inside the function, we should get the index by using the above formula and return the value. One more thing we should take care of is whether the position is valid or not. For example, we have 4 elements and the given position is 6 then it will be invalid. We will check whether the position is valid or not with the if condition. So, inside the if-condition, if Top-Pos+1 < 0, we will print a message that “Invalid Position”. In the else part, we will store the element present at the given position. At the end of the function, we will return the stored value or element. If the value is not found, the function will return -1.

int peek(struct Stack st,int index)
{
    int x=-1;
    if(st.top-index+1<0)
    printf("Invalid Index \n");
    x=st.S[st.top-index+1];

    return x;
}

Now, what time does this function take? The time is constant as we haven’t used any loops here, so all the statements will be executed at a constant time. Now, let us look at three more functions: stackTop (), isEmpty (), and isFull ().

Stack Top() Function:

int stackTop(struct Stack st) {
 if(!isEmpty(st))
    return st.S[st.top];
 return -1;
}

This function will return the topmost value present in the stack.

For example, here, the topmost value is 19. So, wherever Top is pointing, that value will be returned by this function. It takes stack as a parameter. This function will check if Top == -1, return -1 because the stack is empty, and otherwise return the element present at the Top. Here also, the time will be constant. The next function is isEmpty ().

Stack IsEmpty() Function:

int isEmpty(struct Stack st){
 if(st.top==-1)
    return 1;
 return 0;
}

This is also a very simple function. It will also take a stack as a parameter. It will check if top == -1, return 1 means the stack is empty, and otherwise, return 0 means the stack is not empty.

Stack IsFull() Function:

int isFull(struct Stack st) {
 return st.top==st.size-1;
}

This function will check whether the stack is full or not. If the stack is full, it will return true; otherwise, it will return false. It is taking stack as a parameter (call by value). This function will check if top == size – 1, return true because stack is full, otherwise return false means stack is not full.

The time taken by all these functions (stackTop, isEmpty, and isFull) is constant. So, all the operations in the stack that we discussed in this article will take constant time.

Program to Perform Various Operations on Stack using Array in C Language:

#include <stdio.h>
#include <stdlib.h>

struct Stack {
  int size;
  int top;
  int * S;
};

void create(struct Stack * st) {
  printf("Enter Size: ");
  scanf("%d", & st -> size);
  st -> top = -1;
  st -> S = (int * ) malloc(st -> size * sizeof(int));
}

void Display(struct Stack st) {
  int i;
  for (i = st.top; i >= 0; i--)
    printf("%d ", st.S[i]);
  printf("\n");
}

void push(struct Stack * st, int x) {
  if (st -> top == st -> size - 1)
    printf("Stack overflow\n");
  else {
    st -> top++;
    st -> S[st -> top] = x;
  }
}

int pop(struct Stack * st) {
  int x = -1;

  if (st -> top == -1)
    printf("Stack Underflow\n");
  else {
    x = st -> S[st -> top--];
  }
  return x;
}

int peek(struct Stack st, int index) {
  int x = -1;
  if (st.top - index + 1 < 0)
    printf("Invalid Index \n");
  x = st.S[st.top - index + 1];
  return x;
}

int isEmpty(struct Stack st) {
  if (st.top == -1)
    return 1;
  return 0;
}

int isFull(struct Stack st) {
  return st.top == st.size - 1;
}

int stackTop(struct Stack st) {
  if (!isEmpty(st))
    return st.S[st.top];
  return -1;
}

int main() {
  struct Stack st;
  create( & st);

  push( & st, 8);
  push( & st, 12);
  push( & st, 14);
  push( & st, 19);

  printf("Popped Element: %d \n", pop( & st));
  printf("Element at 2nd Position: %d \n", peek(st, 2));
  printf("Element at Top of Stack: %d \n", stackTop(st));
  printf("is stack Empty: %d \n", isEmpty(st));
  printf("is stack Full: %d \n", isFull(st));

  Display(st);

  return 0;
}

Output:

In the next article, I will discuss Stack Implementation using a Linked List in C. In this article, I explain how to Perform Operations on a Stack using an Array in C Language with Examples. I hope you enjoy this article on stacking using an array in C.