Time Series Data in Machine Learning

Back to: Data Science Tutorials

Time Series Data in Machine Learning with Case Study

In this article, I am going to discuss Time Series Data in Machine Learning with Case Study. Please read our previous article where we discussed SVMs in Machine Learning with Examples.

Time Series Data in Machine Learning

A set of observations gathered through repeated measurements over time is known as Time Series Data. If you plot the points on a graph, you’ll notice that one of the axes is always time.

Because time is a component of everything observable, Time Series Data may be found everywhere. Sensors and systems are continually releasing a continuous stream of time series data as our world becomes increasingly instrumented. Such information can be used in a variety of sectors. Let’s look at some examples to put this in context.

Time series analysis examples include:

• The brain’s electrical activity
• Measurements of rainfall
• Prices of stocks
• Sunspots are the number of sunspots on the surface of the sun.
• Retail sales on an annual basis
• Subscribers on a monthly basis
• Minutes of heartbeats

Data from Time Series is collected, stored, displayed, and analyzed for a variety of purposes in a variety of domains:

Time series analysis is used for grouping, classification, query by content, anomaly detection, and forecasting in data mining, pattern recognition, and machine learning.

Time series data is utilized for signal detection and estimation in signal processing, control engineering, and communication engineering.

Time series analysis is used for forecasting in statistics, econometrics, quantitative finance, seismology, meteorology, and geophysics.

To aid insight extraction, trend analysis, and anomaly detection, Time Series Data can be represented in a variety of displays.

Long-term changes in a series are referred to as ‘Time Series Patterns.’ The correlation can be calculated in a variety of ways, depending on whether it is measured as a trend, seasonal pattern, or cyclic pattern (linear, exponential.)

Components of Time Series in Machine Learning

The following are the variables responsible for causing changes in a time series, also known as time series components:

1. Secular/General Trend
2. Seasonal Movements
3. Cyclical Movements
4. Irregular Fluctuations

Secular Trends –

A time series’ secular trend is the main component that emerges from long-term influences of socioeconomic and political issues. This trend can depict the long-term growth or decline of a time series. This is the type of trend that lasts for a very long time. Prices and data on export and import, for example, show clearly growing trends over time.

Seasonal Movements –

These are seasonal data fluctuations that occur over a brief period of time. The short term is often defined as a time span during which changes in a time series occur due to weather or festive events. For example, it is common knowledge that ice-cream consumption is highest during the summer, hence an ice-cream vendor’s sales will be higher during various months of the year and lower during the winter. Variations in weather can affect employment, output, exports, and other factors. Similarly, during festivals such as Valentine’s Day, Eid, Christmas, and New Year’s, the sale of clothing, umbrellas, greeting cards, and fireworks are susceptible to enormous fluctuations. Only when a time series is supplied biannually, quarterly, or monthly are these types of variations isolated.

Cyclic Movements –

Long-term oscillations in a time series are what these are. These oscillations are most commonly seen in economic data, and their periods typically range from five to twelve years or longer. The well-known business cycles are linked to these oscillations. These cyclic movements can be analyzed if a lengthy series of data is available that is free of abnormal disturbances.

Irregular Fluctuations –

These are unexpected changes in a time series that are unlikely to occur again. They’re time-series elements that can’t be explained by trends, seasonal or cyclic motions. Residual or random components are terms used to describe these variances. These differences, albeit unintentional, have the potential to generate a continuous change in trends, and seasonal and cyclical oscillations in the approaching period. Such abnormalities are caused by floods, fires, earthquakes, revolutions, epidemics, strikes, and other natural disasters.

Discuss Different Kinds of Time Series Scenarios in Machine Learning

There are two forms of time series data:

1. Stationary
2. Non-stationary

Stationary Time Series Data –

Without the Trend, Seasonality, Cyclical, and Irregularity components of time series, a dataset should follow the following thumb rules.

1. During the analysis, the MEAN value of them should be entirely constant in the data.
2. With respect to the time frame, the VARIANCE should be constant.
3. COVARIANCE is a metric that assesses the relationship between two variables.

A white noise series is stationary, in the sense that it should seem the same no matter when you look at it. A motionless time series will, in general, have no predictable patterns over time. On-time plots, the series will appear to be generally horizontal (with some cyclic behaviour), with constant variance.

Non-Stationary Time Series Data –

Trends, cycles, random walks, and combinations of the three are examples of non-stationary behaviour. Non-stationary data, by definition, is unexpected and cannot be predicted or modelled. The results acquired using non-stationary time series could be fictitious, implying a relationship between two variables where none exists. Non-stationary data must be turned into stationary data in order to obtain consistent, trustworthy findings.

Working and Implementation of ARIMA Model in Machine Learning

ARIMA (Auto-Regressive Integrated Moving Average) is a class of models that explains a time series based on its own previous values, that is, its own lags and lagged prediction errors, so that equation can be used to anticipate future values. In this free video tutorial, learn more about ARIMA’s parameters and constraints.

ARIMA models can be used to model any ‘non-seasonal’ time series that has patterns and isn’t random white noise. Three terms define an ARIMA model: p, d, and q.

Where

1. p refers to the order of the term AR
2. q refers to the order of the term MA
3. d refers to the number of differencing necessary to make the time series stationary

Now let’s understand the p, d and q terms in the model.

If a time series has seasonal trends, seasonal terms must be added, and the time series becomes SARIMA, short for ‘Seasonal ARIMA.’ After we finish ARIMA, we’ll talk more about it. Making the time series stationary is the first stage in creating an ARIMA model.

Why?

Because the word ‘Auto Regressive’ in ARIMA refers to a linear regression model in which the model’s own lags are used as predictors. As you may be aware, linear regression models function best when the predictors are not correlated and are independent of one another.

So, how do you make a stationary series?

The most popular method is to differentiate it. That is, take the old value and subtract it from the present value. Depending on the complexity of the series, multiple differencing may be required at times. As a result, the value of d is the smallest number of differences required to make the series stationary. And d = 0 if the time series is already stationary.

What are the meanings of the term ‘p’ and ‘q’?

The ‘Auto Regressive’ (AR) term’s order is ‘p.’ It’s the number of Y delays that will be utilized as predictors. The order of the ‘Moving Average’ (MA) word is ‘q.’ It relates to how many lagged forecast mistakes should be included in the ARIMA Model. In English, the ARIMA model is as follows:

Predicted Yt = Constant + Linear Combination of Y Delays (up to p lags) + Lagged Forecast Errors (up to q lags)

The goal is to figure out what the values of p, d, and q are.

In an ARIMA model, how do you find the order of differencing (d)?

The goal of differencing is to bring the time series to a halt. However, you must be cautious not to over-difference the series. Because an over-differenced series may still be stationary, the model parameters will be affected. So, how do you figure out the proper differencing order?

The least differencing required to obtain a near-stationary series that roams around a defined mean and the ACF plot quickly hits zero is the proper sequence of differencing.

If the autocorrelations are positive for a large number of lags (10 or more), the series should be differentiated further. If the lag 1 autocorrelation is too negative, on the other hand, the series is most likely over-differenced. If you can’t decide between two differencing orders, choose the one that results in the least standard deviation in the differenced series.

How can I determine the AR term’s order (p)?

The next stage is to determine whether or not the model requires any AR terms. The required number of AR terms can be determined by looking at the Partial Autocorrelation (PACF) diagram.

But what exactly is PACF?

After removing the contributions from the intermediate lags, partial autocorrelation can be thought of as the correlation between the series and its lag. As a result, PACF encapsulates the pure correlation between a lag and a series. In such a way, you’ll know whether or not that lag is required in the AR term.

How do I figure out what sequence the MA terms are in? (q)

You may look at the ACF plot for the number of MA terms in the same way that we looked at the PACF plot for the number of AR terms. Technically, the error of the lagged forecast is referred to as an MA term. The ACF indicates the number of MA terms required to remove any autocorrelation from the stationarized series.

Time Series Analysis Case Study in Machine Learning

Problem Statement

Fundamental and technical analysis are the two main components of stock market analysis. Fundamental analysis is the process of determining a company’s future profitability based on its existing business environment and financial performance.

Technical analysis, on the other hand, entails interpreting charts and analysing statistical data to determine stock market patterns.

As you may expect, we’ll concentrate on the technical analysis portion. We’ll be utilising a Quandl dataset (you can access historical data for other stocks here), and I’ve chosen the data for ‘Tata Global Beverages’ for this project. It’s time to get right in!

Importing Libraries

#import packages
import pandas as pd
import numpy as np

#to plot within notebook
import matplotlib.pyplot as plt
%matplotlib inline

#setting figure size
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 20,10

#for normalizing data
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))

#read the file
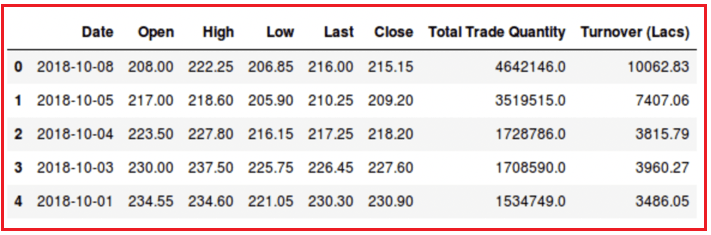
df = pd.read_csv('NSE-TATAGLOBAL(1).csv')

#print the head
df.head()

#setting index as date
df['Date'] = pd.to_datetime(df.Date,format='%Y-%m-%d')
df.index = df['Date']

#plot
plt.figure(figsize=(16,8))
plt.plot(df['Close'], label='Close Price history')

Moving Average

data = df.sort_index(ascending=True, axis=0)
new_data = pd.DataFrame(index=range(0,len(df)),columns=['Date', 'Close'])

for i in range(0,len(data)):
    new_data['Date'][i] = data['Date'][i]
    new_data['Close'][i] = data['Close'][i]

# NOTE: While splitting the data into train and validation set, we cannot use random splitting since that will destroy the time component. So here we have set the last year’s data into validation and the 4 years’ data before that into train set.

# splitting into train and validation
train = new_data[:987]
valid = new_data[987:]

# shapes of training set
print('\n Shape of training set:')
print(train.shape)

# shapes of validation set
print('\n Shape of validation set:')
print(valid.shape)

# In the next step, we will create predictions for the validation set and check the RMSE using the actual values.
# making predictions
preds = []
for i in range(0,valid.shape[0]):
   a = train['Close'][len(train)-248+i:].sum() + sum(preds)
   b = a/248
   preds.append(b)

# checking the results (RMSE value)
rms=np.sqrt(np.mean(np.power((np.array(valid['Close'])-preds),2)))
print('\n RMSE value on validation set:')
print(rms)

#plot
valid['Predictions'] = 0
valid['Predictions'] = preds
plt.plot(train['Close'])
plt.plot(valid[['Close', 'Predictions']])

ARIMA

from pyramid.arima import auto_arima

data = df.sort_index(ascending=True, axis=0)

train = data[:987]
valid = data[987:]

training = train['Close']
validation = valid['Close']

model = auto_arima(training, start_p=1, start_q=1,max_p=3, max_q=3, m=12,start_P=0, seasonal=True,d=1, D=1, trace=True,error_action='ignore',suppress_warnings=True)
model.fit(training)

rms=np.sqrt(np.mean(np.power((np.array(valid['Close'])-np.array(forecast['Prediction'])),2)))
rms

plt.plot(train['Close'])
plt.plot(valid['Close'])
plt.plot(forecast['Prediction'])

In the next article, I am going to discuss ETS Models in Machine Learning with Examples. Here, in this article, I try to explain Time Series Data in Machine Learning with Case Study. I hope you enjoy this Time Series Data in Machine Learning with Case Study article.