Back to: Data Science Tutorials
Inferential Statistics in Data Science
In this article, I am going to discuss Inferential Statistics in Data Science. Please read our previous article where we discussed Descriptive Statistics in Data Science. At the end of this article, you will understand the following pointers in detail which are related to Inferential Statistics in Data Science.
- What are Inferential Statistics
- What is Hypothesis Testing
- Confidence Level
- Degrees of freedom
- What is pValue?
- Chi-Square Test
- What is ANOVA
- Correlation vs Regression
- Use cases
What are Inferential Statistics in Data Science?
Descriptive statistics describe data (such as a chart or graph), whereas inferential statistics in data science allows you to make predictions (“inferences”) based on that data. Inferential statistics are used to make generalizations about a population based on data from samples.
For example, you could stand in a mall and poll 100 people to see if they like shopping at Sears. You could create a bar chart with yes/no responses (descriptive statistics), or you could use your research (and inferential statistics) to conclude that 75-80 percent of the population (all shoppers in all malls) enjoy shopping at Sears.
Inferential statistics are divided into two categories:
- Parameter estimation: This entails using a statistic from your sample data (for example, the sample mean) to make a statement about a population parameter (i.e. the population mean).
- Hypothesis tests are performed: This is where sample data can be used to answer research questions. For example, you might be curious about the efficacy of a new cancer drug. Or if breakfast improves children’s academic performance.
What is Hypothesis Testing?
The primary goal of statistics is to test hypotheses. For example, you could conduct an experiment and discover that a particular drug is effective at treating headaches. However, if you are unable to replicate the experiment, no one will take your findings seriously.
A hypothesis is an educated guess about something in your environment. It should be testable, either experimentally or through observation. As an example:
- A new medication that you believe may be effective.
- A method of teaching that you believe would be more effective.
- A possible new species’ habitat.
- A more equitable method of administering standardized tests.
- It can really be anything as long as it can be put to the test.
In statistics, hypothesis testing is a method of determining whether the results of a survey or experiment are meaningful. By calculating the odds that your results occurred by chance, you are essentially testing whether your results are valid. If your results were purely coincidental, the experiment will be unrepeatable and thus of little use.
Hypothesis testing can be one of the most perplexing aspects for students, owing to the fact that before you can even perform a test, you must first determine what your null hypothesis is. Those tricky word problems that you are presented with can often be difficult to decipher.
But it’s not as difficult as you think; all you have to do is:
- Determine your null hypothesis.
- Describe your null hypothesis.
- Choose the type of test you need to run, either supporting or rejecting the null hypothesis.
If you go back in time in science, the null hypothesis has always been the accepted fact. Simple examples of null hypotheses that are widely accepted as true include:
- DNA has the shape of a double helix.
- The solar system contains eight planets (excluding Pluto).
- Taking Vioxx may increase your chances of developing heart problems (a drug now taken off the market).
Hypothesis Example
In this question, the researcher’s hypothesis is that the average recovery time is longer than 8.2 weeks. In mathematical terms, it is as follows: H1: > 8.2
The null hypothesis must then be stated. That is what will occur if the researcher is incorrect. If the researcher is incorrect in the preceding example, the recovery time is less than or equal to 8.2 weeks. In math, this is:
H0 μ ≤ 8.2
We thought the solar system had nine planets about ten years ago. Pluto was demoted to the status of planet in 2006. The null hypothesis of “Pluto is a planet” was replaced by the null hypothesis of “Pluto is not a planet.” Of course, rejecting the null hypothesis isn’t always so simple—the most difficult part is usually determining what your null hypothesis is in the first place.
Hypothesis Example (One sample Z-Test)
A principal at one school claims that his students have above-average intelligence. The mean IQ score of a random sample of thirty students is 112.5. Is there enough evidence to back up the principal’s claim? The population’s average IQ is 100, with a standard deviation of 15.
Step1: It is to state the Null hypothesis. The population mean is accepted to be 100
Step2: Describe the Alternative Hypothesis. The claim is that the students have higher-than-average IQs, so H1: > 100.
Because we are looking for scores “greater than” a certain point, this is a one-tailed test.
Step3: Make a drawing to help you visualize the problem.
Step4: Specify the alpha level. If you are not given an alpha level, use 5%. (0.05).
Step5: Find the rejection region area from the z-table (given by your alpha level above). A z-score of 1.645 corresponds to an area of 0.05
Step6: Using this formula, calculate the test statistic:
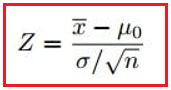
Step7: If Step 6 is greater than Step 5, the null hypothesis is rejected. If it is less than Step 5, the null hypothesis cannot be rejected. In this case, it is greater (4.56 > 1.645), so the null can be rejected.
Bayesian Hypothesis Testing
Bayesian hypothesis testing can assist in answering the question, “Can the results of a test or survey be repeated?”
What difference does it make if a test can be repeated? Assume that twenty people in the same village were diagnosed with leukemia. Cell phone towers, according to a group of researchers, are to blame. A second study, however, discovered that cell phone towers had nothing to do with the cancer cluster in the village. In fact, they discovered that the cancers were entirely random. Even if it seems impossible, it is possible! Cancer clusters can occur simply by chance. There could be a variety of reasons why the first study was flawed.
It’s good science to let people know whether your study’s findings are solid or if they could have happened by chance. The standard method is to use a p-value to test your results. A p-value is a number obtained by performing a hypothesis test on your data. A P value of 0.05 (5%) or less is usually sufficient to assert that your results are repeatable. There is, however, another method for testing the validity of your results: Bayesian Hypothesis testing. This type of testing allows you to test the strength of your results in a different way.
Non-Bayesian testing refers to traditional testing (the type you probably encountered in elementary or AP statistics). It is the frequency with which an outcome occurs over repeated runs of the experiment. It provides an objective assessment of whether an experiment is repeatable.
Bayesian hypothesis testing is a subjective interpretation of the same concept. It considers how confident you are in your results. To put it another way, would you bet money on the outcome of your experiment?
Confidence Level

When a poll is reported in the media, the results frequently include a confidence level. A survey, for example, might report a 95 percent confidence level. But what does this actually mean? At first glance, you might think it means it’s 95% accurate. That is close to the truth, but as with many statistics, it is actually a little more defined.
For example, according to a recent Rasmussen Reports article, “38 percent of Likely U.S. Voters now say their health insurance coverage has changed as a result of Obamacare.” You can find this line at the bottom of the article: “The margin of sampling error is +/- 3 percentage points with a 95 percent level of confidence.”
It is impractical to poll all 300 million or so U.S. residents, so it is impossible to know how many people would actually respond “yes, my health insurance has changed.” We take a sample (say, 2,000 people) and use good statistical techniques such as simple random sampling to make our “best guess” at what the actual figure is (we call that unknown figure a population parameter). A 95 percent confidence level means that the results of the poll or survey would match the results of the actual population 95 percent of the time if it were repeated many times.
The width of the confidence interval tells us how certain (or uncertain) we are about the true population figure. The width of the confidence interval is expressed as a plus or minus (in this case, +/- 3). When you combine the interval and the confidence level, you get a percentage spread. In this case, you would expect the results to be between 35 (38-3) and 41 (35+3) percent of the time.
Factors Influencing Confidence Intervals (CI)
Population size: this does not usually affect the CI, but it can be a consideration if you are working with small and well-known groups of people.
- Sample Size: The smaller the sample, the less likely you can be confident that the results accurately reflect the true population parameter.
- Percentage: Extreme answers are more accurate. For example, if 99 percent of voters support gay marriage, the margin for error is slim. However, if 49.9 percent of voters vote “for” and 50.1 percent vote “against,” the margin of error increases.
A confidence level of 0% indicates that you have no faith that the same results would be obtained if the survey were repeated. A confidence level of 100 percent indicates that there is no doubt that the same results would be obtained if the survey were repeated. In reality, you would never publish the results of a survey if you had any doubts about the accuracy of the statistics (you would probably repeat the survey with better techniques). A 100 percent confidence level does not exist in statistics unless you survey an entire population — and even then, you can’t be certain that your survey was free of error or bias.
Degree of Freedom
The number of independent pieces of information used to calculate an estimate is referred to as its degrees of freedom. It isn’t exactly the same as the number of items in the sample. To calculate the df for the estimate, subtract 1 from the number of items. Assume you were looking for the average weight loss on a low-carb diet. You could use four people, resulting in three degrees of freedom (4 – 1 = three), or one hundred people, resulting in df = 99.
Degrees of Freedom = n – 1
Why do we deduct one from the total number of items?
Degrees of freedom can also be defined as the number of values in a data set that is free to vary. What does it mean to be “free to vary”? Here’s an example of how to use the mean (average):
Q. Choose a set of numbers with a mean (average) of 10.
A. You could choose from the following sets of numbers: 9, 10, 11 or 8, 10, 12 or 5, 10, 15.
The third number in the set is fixed once you’ve chosen the first two. In other words, you are unable to select the third item in the set. The first two numbers are the only ones that can be changed. You can choose 9 + 10 or 5 + 15, but once you’ve decided, you must choose a specific number that will give you the mean you’re looking for. As a result, the degree of freedom for a set of three numbers is TWO.
For instance, if you want to find a confidence interval for a sample, the degree of freedom is n – 1. The number “N” can also represent the number of classes or categories.
If you have two samples and want to find a parameter, such as the mean, you must consider two “n”s (sample 1 and sample 2). In that case, the degrees of freedom are:
Degrees of Freedom (Two Samples): (N1 + N2) – 2.
Degree of Freedom in ANOVA
In ANOVA tests, degrees of freedom become a little more complicated. ANOVA tests compare known means in data sets rather than a simple parameter (such as finding a mean). In a one-way ANOVA, for example, you are comparing two means in two cells. The grand mean (the average of the averages) is as follows:
The sum of mean 1 and mean 2 is the grand mean.
What if you picked mean 1 and already knew the grand mean? Because you wouldn’t be able to choose Mean2, your degree of freedom for a two-group ANOVA is 1.
What is P-Value?
The p-value in statistics is the probability of obtaining results that are at least as extreme as the observed results of a statistical hypothesis test, assuming that the null hypothesis is correct. The p-value is used instead of rejection points to provide the smallest level of significance at which the null hypothesis is rejected. A lower p-value indicates that there is more evidence supporting the alternative hypothesis.
P-values are typically calculated using p-value tables or spreadsheet/statistical software. These calculations are based on the assumed or known probability distribution of the statistic under consideration. Given the probability distribution of the statistic, p-values are calculated as the difference between the observed value and a chosen reference value, with a greater difference between the two values corresponding to a lower p-value.
The p-value is calculated mathematically from the area under the probability distribution curve for all statistics values that are at least as far from the reference value as the observed value is, relative to the total area under the probability distribution curve, using integral calculus. In a nutshell, the greater the difference between two observed values, the less likely the difference is due to random chance, as reflected by a lower p-value.
The calculated probability is used in the p-value approach to hypothesis testing to determine whether there is evidence to reject the null hypothesis. The null hypothesis, also known as the conjecture, is the first statement made about a population (or data generating process). The alternative hypothesis states whether or not the population parameter differs from the value stated in the conjecture.
In practice, the significance level is specified ahead of time to determine how small the p-value must be to reject the null hypothesis. Because different researchers use different levels of significance when examining a question, a reader may occasionally struggle to compare results from two different tests. P-values offer a solution to this issue.
For example, suppose two researchers conducted a study comparing the returns on two different assets using the same data but at different significance levels. The researchers may reach opposing conclusions about whether the assets differ. If one researcher used a confidence level of 90% and the other required a confidence level of 95% to reject the null hypothesis, and the p-value of the observed difference between the two returns was 0.08 (corresponding to a confidence level of 92%), the first researcher would conclude that the two assets have a statistically significant difference, while the second would conclude that the difference is not statistically significant.
Chi-Square Test Inferential Statistics in Data Science
A Chi-square test is a method for testing hypotheses. Two popular Chi-square tests involve determining whether the observed frequencies in one or more categories match the expected frequencies. There are two commonly used Chi-square tests: the Chi-square goodness of fit test and the Chi-square test of independence.
The same analysis steps are used for both the Chi-square goodness of fit test and the Chi-square test of independence, which are listed below.
- Before collecting data, define your null and alternative hypotheses.
- Choose an alpha value. This entails deciding how much risk you are willing to take in drawing the incorrect conclusion. Assume, for example, that you set =0.05 when testing for independence. You have decided to take a 5% chance of concluding that the two variables are independent when they are not.
- Examine the data for errors.
- Examine the test assumptions. (For more information on assumptions, see the pages for each test type.)
- Carry out the experiment and reach your conclusion.
The basic concept behind the tests is to compare the actual data values to what would be expected if the null hypothesis is true. Finding the squared difference between actual and expected data values and dividing that difference by the expected data values yields the test statistic. This is repeated for each data point, and the values are totaled.
Correlation and Regression Inferential Statistics in Data Science
The two multivariate distribution-based analyses are correlation and regression. The term “multivariate distribution” refers to a distribution with multiple variables. Correlation is defined as the analysis that determines the existence or absence of a relationship between two variables ‘x’ and ‘y.’
Regression analysis, on the other hand, predicts the value of the dependent variable based on the known value of the independent variable, assuming an average mathematical relationship exists between two or more variables.
Correlation is derived from the words ‘Co’ (together) and the relationship between two quantities. Correlation occurs when it is observed that a change in one variable’s unit is retaliated by an equivalent change in another variable, either directly or indirectly, during the study of two variables. Alternatively, the variables are said to be uncorrelated when there is no movement in one variable that corresponds to any movement in another variable in a specific direction. It is a statistical technique used to represent the strength of the relationship between two variables.
Correlation can be both positive and negative. If the two variables move in the same direction, i.e. an increase in one variable causes an increase in the other, and vice versa, the variables are said to be positively correlated. As an example, consider the terms investment and profit.
A negative correlation occurs when the two variables move in opposite directions, such that an increase in one variable causes a decrease in the other, and vice versa. For instance, consider the price and demand for a product.
Regression is a statistical technique for estimating the change in the metric dependent variable due to a change in one or more independent variables that are based on the average mathematical relationship between two or more variables. It is an important tool in many human activities because it is a powerful and versatile tool for forecasting past, present, or future events based on past or present events. For example, a company’s future profit can be estimated based on past performance.
In simple linear regression, there are two variables, x, and y, where y depends on x or is influenced by x. In this case, y is referred to as a variable dependent or criterion, and x is referred to as a variable independent or predictor. The line of regression y on x is written as follows:
Y = a + bx
where, a = constant,
b = regression coefficient, a and b are the two regression parameters in this equation.
Here’s what the distinction between correlation and regression analysis is. To summarize, there are four key differences between those terms.
- When it comes to correlation, there is a relationship between the variables. Regression, on the other hand, focuses on how one variable affects the other.
- Correlation, which is based on regression, does not capture causality.
- The correlation between x and y is the same as the correlation between y and x. In contrast, a regression of x and y, as well as y and x, yields completely different results.
- Finally, a single point can be used to represent a correlation graphically. A single line represents a linear regression.
In the next article, I am going to discuss Python Programming. Here, in this article, I try to explain Inferential Statistics in Data Science and I hope you enjoy this Inferential Statistics in Data Science article. I would like to have your feedback. Please post your feedback, question, or comments about this Inferential Statistics in Data Science article.
Registration Open – Microservices with ASP.NET Core Web API
Session Time: 6:30 AM – 8:00 AM IST
Advance your career with our expert-led, hands-on live training program. Get complete course details, the syllabus, registration, and Zoom credentials for demo sessions via the links below.

