Introduction to Tree Data Structure

Back to: Data Structures and Algorithms Tutorials

Introduction to Tree Data Structure:

In this article, I will give a brief Introduction to Tree Data Structure. We will discuss various types of trees, such as general trees and binary trees. Then, we will learn about tree terminology.

Tree Terminologies:

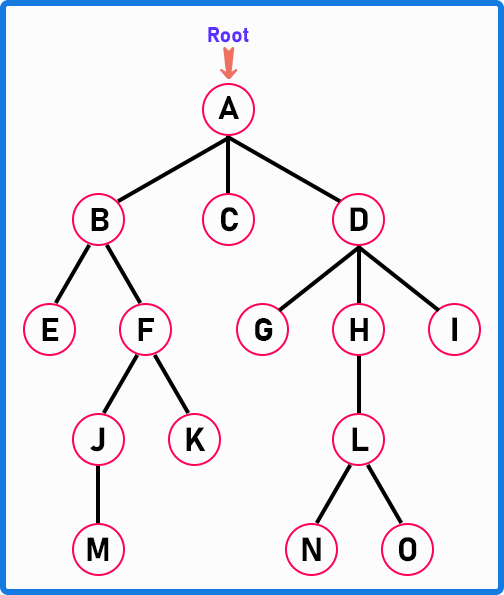
Here, we have taken a general tree in which nodes are represented by alphabets, making it easy for you to understand.

What is a Tree?

A Tree is a hierarchical data structure consisting of nodes, each with a value and zero or more child nodes. It represents a set of hierarchical relationships, with one node at the top called the root and all other nodes as descendants of this root. Trees are used to model hierarchical relationships in data. So, a Tree is a collection of Nodes (circles) and Edges (lines). The links between the nodes are known as edges.

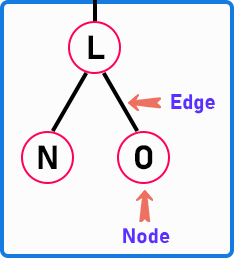
If there are ‘n’ nodes (vertices), there will be ‘n-1’ edges in a tree because each node’s edge comes from the parent node except the root node.

What is a Root Node?

The Root Node is the topmost node in a tree. It is the starting point of the tree, and it is the only node in the tree that does not have a parent. Every tree has exactly one root node. All other nodes in the tree are descendants of the root node. The very first node of a tree is the root node. It is the tree’s parent node, or we can say the tree’s origin.

What is a Subtree?

A subtree is a portion of a tree structure that consists of a node and all its descendants. For example, if you select any node and consider it as the root of a new tree, the resulting structure is called a subtree. A subtree is a collection of nodes that come under nodes ‘B,’ C,’ or ‘D’.

These three different colors represent three different subsets of a tree. A tree is a collection of nodes, with one node being the root node and the rest divided into disjoint subsets. Each subset is itself a tree or subtree.

What is a Parent Node?

A Parent Node is a node in a tree that has one or more child nodes directly connected to it. It is the immediate predecessor of its child nodes. In other words, it is a node that is one level above another node in the hierarchy. For example, F is a parent node of J, and K. D is a parent node of G, H, and I.

What is a Child Node?

A Child Node is a node in a tree directly connected to another node, known as its parent. Each child node can, in turn, be a parent to its child nodes. Each child. For example, B, C, and D are child nodes of A.

What are Sibling Nodes?

Sibling Nodes are nodes in a Tree that share the same parent node. They are located at the same level in the tree and are directly connected to the same parent or are direct children of the same parent node. For example, J and K are children of F, so they are siblings. B, C, and D are children of A, so they are siblings.

Descendants:

Descendants refer to all the nodes reachable from a particular node, including its immediate children, their children, and so on down the hierarchy. Essentially, descendants are all nodes in the subtree rooted at a given node, excluding the node itself. For example, E, F, J, K, and M are the descendants of B. G, H, I, L, N, and O are descendants of D.

Ancestors:

Ancestors refer to all the nodes on the path from a given node up to the tree’s root node. Each node (except the root node) has one or more ancestors, which are its parent node, its parent’s parent, and so on, until reaching the root node. For example, J, F, B & A are ancestors of node M. L, H, D & A are ancestors of node N.

What is the Degree of a Node?

The Degree of a Node is the number of children that a node has. A node with no children has a degree of zero, while a node with three children has a degree of three. Direct children will be considered, not descendants. For example:

• If a node has no children, its degree is 0 (it is a leaf node).
• If a node has one child, its degree is 1.
• If a node has two or more children, its degree equals the number of children.

The degree of a node in a tree helps determine its position and relationship within the hierarchical structure.

For example, Degree of A: 3, B: 2, F: 2, J: 1, D: 3, H: 1, L: 2

What is the degree of a tree?

The Degree of a Tree is the maximum degree of any node within the tree. It represents the maximum number of children any node in the tree has. If you observe, what is the maximum degree of any node? 3. So, the degree of a tree can be a minimum of 3.

What are Internal Nodes?

An internal node, also known as a non-leaf node, is a node that has at least one child node. In other words, it is a node that is not a leaf node, meaning it has descendants. These are also known as non-terminal nodes. For example, A, B, C, D, F, H, J & L are internal nodes.

What are External Nodes (Leaf Nodes)?

An external node, also known as a leaf node, is a node that has no children. It is located at the tree structure’s periphery and has no descendants. These nodes are also known as terminal nodes. For example, E, M, K, C, G, I, N & O are terminal nodes.

What are the Levels of a Tree?

Levels of a tree refer to the hierarchical levels of nodes starting from the root node. The root is at level 1, its children are at level 2, the children of those nodes are at level 3, and so forth.

For level, we count only nodes. We take the path by counting the number of nodes.

What is the Height of a Tree?

The Height of a Tree is the length of the longest path from the root to a leaf node. It is the number of edges on the longest path from the root to a leaf. The height of a tree with only one node (the root) is 0. The height of a tree starts from 0 onwards. The root is numbered 0, and its children are at level 1, and their children are at level 2, and so on.

For height, we count edges. So, levels start from 1 onwards, and height starts from 0 onwards. Height and level are both useful for analysis.

What is a Forest?

A Forest is a collection of disjoint trees. In other words, it is a set of trees that do not share any common nodes. A forest can be thought of as a set of separate trees. If you remove the root of a tree, the remaining subtrees form a forest.

In the above diagram, there are three trees, which is known as a forest. If you combine them with a root node, the forest will become a tree. If there is a root node connected to all the trees, the forest will become a tree. That’s all. These are some basic terminologies about a tree. Now, let us introduce you to a binary tree.

What is a Binary Tree?

A Binary Tree is a tree in which each node has at most two children, often referred to as the left and right child. Binary trees are used in various applications, such as binary search, heaps, and expression trees.

A tree of degree 2 means every node can have a maximum of 2 children. It can have fewer than two children but not more than 2; then, it is called a binary tree. Every node can have two or fewer than two children. For example, A has two child nodes, B & C. Then, B and C have two child nodes: D and E and F and G. As there are only two children of a node, we can give them names like the left child and the right child.

So, every node can have either 0 children, one child, or at most two children.

Children = {0, 1, 2}

Let us look at some examples of binary trees.

Now, let us examine which one is a binary tree and why.

1. (I): It is a binary tree as two nodes have two child nodes, and three nodes have no child. So, it satisfies the condition of a binary tree.
2. (II): It is a binary tree as two nodes have one child node, and one node has 0 children. This type of tree is also known as a right-skewed tree.
3. (III): It is a binary tree as two nodes have one child node, and one node has 0 children. This type of tree is also known as a left-skewed tree.
4. (IV): This is not a binary tree, as the root node has three child nodes, and binary trees allow only two or fewer children.
5. (V): This is a binary tree, as every node has two child nodes except terminal nodes.

Binary trees are more commonly used, and various forms of binary trees exist. We will learn about them in upcoming articles.

In the next article, I will discuss Binary Trees in C Language with Examples. In this article, I give a brief Introduction to a Tree Data Structure. I hope you enjoy this article on Introduction to Tree Data Structure.