Back to: C++ Tutorials For Beginners and Professionals
Introduction to Number System
In this article, we are going to give a brief introduction to the number system. In the previous article, we discuss how a computer works and at the end, we conclude that all electronic machines use a binary system that is zeros and ones or on and off, but we as human beings understand the decimal number system.
Number System:
Firstly, let us know why we need to understand the Number System while we are learning a programming language. The Number System, which we Humans follow, is the Decimal number system but the computer understands in Binary number system. So again, there is a difference between how I saw the number and how the computer sees it.
Example:
As a human, if I give 10 for me it is Ten but for the computer, it is two. So, it’s actually necessary to understand the different types of number systems.
- Binary Number System: {0,1}
- Octal Number System: {0,1,2,3,4,5,6,7}
- Decimal number system: {0.1,2,3,4,5,6,7,8,9}
- Hexadecimal number system: {0,1,2,3,4,5,6,7,8,9,10, A, B, C, D, E, F}
Basically, we use the decimal system and in the decimal number system, the pictures or figures or the symbols are from 0 to 9 i.e. total of 10 symbols we have. As we already discussed the computer works on zeros and ones. So, for computers, there are only two symbols and the binary number systems have only two symbols i.e. 0 and 1.
In the decimal number system, once we have finished with the last symbol i.e. 9, after 9, we use the combination of symbols (from 0 to 9). For example- 10, 11, 12, and so on. 10 is the combination of two symbols i.e. 0 and 1 similarly 11 is the combination of 1 and 1.
So, the point that you need to understand is, once we finished with the symbols, then we can take the combination of symbols and in the binary number system, the same methodology is also followed. To denote the new number, we use the combinations of two symbols i.e. 1’s and 0’s. For example, to denote 2 in the binary system we will use the combination of 1 and 0 i.e. 10, don’t read it as ten, read it as one zero. For more details, please have a look at the following which shows the numbers from 0 to 16 in the Decimal, Binary, Hexadecimal, and Octal number system.
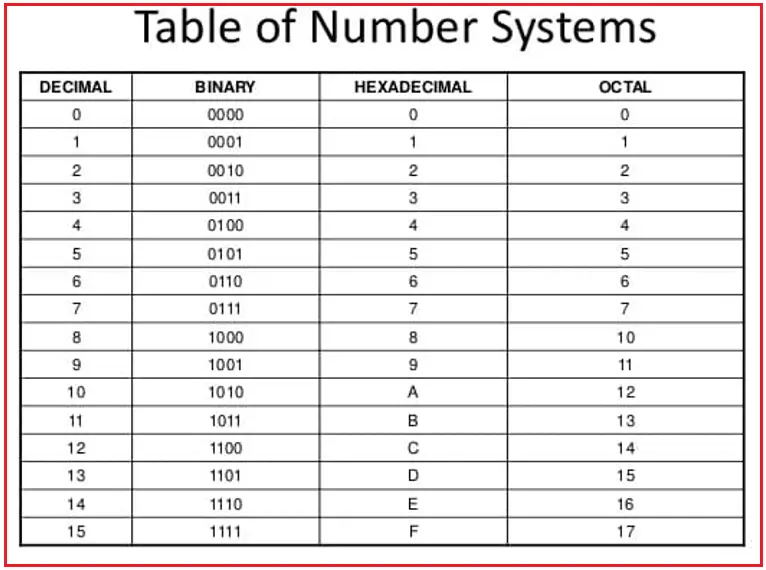
The above table gives how we see numbers in each number system. However, one thing here is common when we exceed the number then the combination of numbers will come. For Example, in the decimal system 0 to 9 after nine, ten is a combination of first and second i.e. 0, and 1 i.e. 10. Similar is holds good for other number systems. There is a separate chapter where we will discuss the conversion of one number system to another number system in detail.
We discussed binary and Decimal number systems, then what is these hexadecimal and octal number system. See, remembering a number as 0, 0, 1, 1 is too top. We need a simple method. So, what people have done, to make decimal and binary number systems simple, octal number system introduced. Let’s, look at how we convert Decimal numbers to a binary system.
How to Convert Decimal Number to Binary Number?
For example- 29 is the decimal number and let’s see how we can convert this decimal number into a binary number. As we discussed the base for the binary number is 2 and hence, we need to perform successive division 2 and take the remainder and then read the remainders from bottom to top to get the binary number as shown in the below image.

This is the binary form. so, this is how a decimal number is converted into binary. We learned about converting decimal to a binary system. Now, we will see how to convert a binary number to decimal form. For example – 10101 is the binary number and we need to find out its equivalent decimal number. For a better understanding, of how to convert please have a look at the following diagram.

Let us see the procedure.
1 0 1 0 1 = 1 * 24 + 0*23 + 1*22 + 0*21 + 1*20
This will give us – 16+0+4+0+1 = 21
So, this is how we can convert a binary number to a decimal number. We have seen how to convert decimal numbers to binary and binary numbers back to decimals using pen paper. Now electronic circuitry internally handles these things. For humans, we follow these conversion methods to understand how it is represented in binary form. So, knowing the number system will help in the future.
Note: In our upcoming articles, once we start programming, we will see programs for all these conversations.
In the next article, I am going to give an overview of High-level and Low-level Programming Languages. Here, in this article, I try to give a brief introduction to the Number System and I hope you enjoy this Number System article.
