Infix to Postfix using Stack in C

Back to: Data Structures and Algorithms Tutorials

Infix to Postfix using Stack in C:

In this article, I will discuss Infix to Postfix using Stack in C with Examples. Please read our previous article discussing Associativity and Unary Operators in C.

Infix to Postfix using Stack Method 1:

Now, we will understand the procedure for converting an infix expression into a postfix expression using a stack.

Here, we have an infix expression. This expression has only a few operators: +, *, -, and /. The precedence and associativity for these operators are given below.

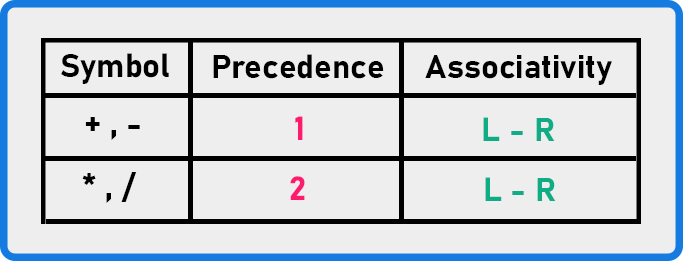
If you want to include more operators, you can increase the size of the table and add their precedence. However, to understand the procedure, we are taking a small and simple example. Let’s see how to convert this expression.

Procedure for Conversion of Infix to Postfix using Stack:

We will use a stack to demonstrate the procedure.

We have an empty stack, and our goal is to generate a postfix expression. Now, we need to scan the expression, taking one symbol at a time.

The first symbol is ‘a’, which is an operand. Whenever we encounter an operand, we write it in the postfix expression.

Postfix: a

The next symbol is ‘+’, which is an operator. The precedence of addition is 1. Since the stack is empty, we push ‘+’ into the stack.

The next symbol is ‘b’. So, we write it in the postfix expression.

Postfix: a b

The next symbol is ‘*’. The precedence of multiplication is 2. Now, we have to check if there are any symbols inside the stack. Yes, there is a plus symbol with precedence 1. However, multiplication has a higher precedence, i.e., 2. So, we’ll push ‘*’ into the stack.

The next symbol is ‘c’. We write it in the postfix expression.

Postfix: a b c

The next symbol is ‘-‘. The precedence of subtraction is 1. On top of the stack, there is a multiplication operator with precedence 2. Since the precedence of subtraction is smaller than that of multiplication, we pop out ‘*’ and write it in the postfix expression.

Postfix: a b c *

Now, we check the precedence of subtraction with addition. They both have equal precedence, which is 1. So, if the precedence is smaller or equal, then we pop out the symbol from the stack. Therefore, we pop out ‘+’ and write it in postfix.

Postfix: a b c * +

Now, the stack is empty, so we push ‘-‘ into the stack.

The next symbol is ‘d’. So, we write it in the postfix expression.

Postfix: a b c * + d

Now, the symbol is ‘/’. The precedence of division is 2. We need to check if there are any symbols inside the stack. Yes, subtraction is there with precedence 1. Since division has higher precedence, we push ‘/’ into the stack.

The next symbol is ‘e’, which is an operand. So, we write it in the postfix expression.

Postfix: a b c * + d e

Now, no symbols are left in the expression. We’ve reached the end of the expression. So, whatever symbols are present in the stack, we pop out all of them and write them in the postfix expression.

First, we pop out the division and then subtraction.

Postfix: a b c * + d e / –

Now, the stack is empty, and we have our postfix expression. Below are the key steps of this procedure:

Steps to Perform the Conversion of Infix to Postfix:

Step 1: If the symbol is an operand, write it in postfix.

Step 2: If the symbol is an operator, there are 3 conditions:

• If the stack is empty, push the symbol onto the stack.
• If the topmost symbol on the stack has lower precedence than the current symbol, push the current symbol onto the stack.
• If the topmost symbol on the stack has higher or equal precedence compared to the current symbol, pop out the symbol from the stack and write it in postfix. Then, check if there are any symbols remaining in the stack. If yes, check their precedence and perform the above steps accordingly.

Step 3: If you have reached the end of the expression and the stack is not empty, pop out all the symbols from the stack and write them in postfix in the same manner as before.

Explanation with the help of a Table:

Usually, when we have an iterative procedure, we prepare a table for that. Let’s prepare a table and show you step by step what is happening in the procedure.

Now, we’ll illustrate the procedure step by step using the table above.

Symbol: a

Initially, there’s nothing inside the stack. So, the operand ‘a’ is written in postfix.

Symbol: +

Here, ‘+’ is pushed into the stack, and the postfix expression remains the same.

Symbol: b

‘b’ is an operand, so we’ve appended it in postfix.

Symbol: *

‘*’ is an operator. We’ve pushed it into the stack because it has higher precedence than ‘+’.

Symbol: c

‘c’ is an operand so we’ve appended it in postfix.

Symbol: –

‘-‘ is an operator. It has lower precedence than ‘*’, and equal precedence with ‘+’. So, we’ve popped out both of these symbols and appended them in postfix. Finally, ‘-‘ is pushed into the stack.

Symbol: d

‘d’ is an operand. It has been appended in postfix.

Symbol: /

‘/’ is an operator and has higher precedence than ‘-‘. So, we have pushed it into the stack.

Symbol: e

‘e’ is an operand. It has been appended in postfix.

Here, we have popped out the remaining symbols from the stack and appended them in the postfix expression. You can see each step in this table.

Infix to Postfix using Stack Method 2:

Now, we’ll look at the procedure once again with some minor changes.

The precedence table had addition, subtraction, multiplication, and division. Now, we have included variables or operands. Here, we’re assuming that operands have higher precedence, which is 3. This means operands and operators will be pushed into the stack. Let us see how the procedure works.

Procedure for Conversion of Infix to Postfix using Stack:

In the procedure, every symbol from the expression will go into the stack. In the first method that we discussed in the previous article, we’re only pushing the operators and appending the operands in the postfix expression. But now, every symbol will be pushed into the stack. Let’s see how it works. Here, we’re taking an empty stack and the same expression as in the previous article.

The first symbol is ‘a’. It is an operand with a precedence of 3 (as per the above table).

Now, the stack is empty. So, we’ll push ‘a’ into the stack.

Now, the next symbol is ‘+’. ‘+’ has the precedence of 1 and ‘a’ has the precedence of ‘3’. It means ‘a’ has higher precedence. In this method, if a symbol that has equal or higher precedence than the current symbol is present in the stack, we’ll pop out that symbol. So, we’ll pop out ‘a’, append it in postfix expression, and push ‘+ into the stack.

Postfix: a

The next symbol is ‘b’. ‘b’ has higher precedence (3) than ‘+’ (1). So, put ‘b’ into the stack.

The next is ‘*’. ‘*’ has lower precedence than ‘b’. So, we’ll pop out ‘b’, append it in postfix expression.

Postfix: a b

After popping out ‘b’, ‘+’ is inside the stack. ‘*’ has higher precedence than’+’. So, we’ll push ‘*’ into the stack.

The next symbol is ‘c’. ‘c’ has higher precedence than ‘*’. So, push ‘c’ into the stack.

The next symbol is ‘-‘. ‘-‘ has lower precedence than ‘c’. So, we’ll pop out and append it in Postfix.

Postfix: a b c

Now, ‘-‘ has lower precedence than ‘*’. So, again, we’ll pop out ‘*’ and append it in postfix.

Postfix: a b c *

Here, ‘-‘ and ‘+’ have the same precedence. So, again, pop out and append ‘+’ in postfix.

Postfix: a b c * +

As the stack is empty, so now we can push ‘-‘ into the stack.

Now, the next symbol is ‘d’. ‘d’ has higher precedence than ‘-‘. So, we’ll push ‘d’ into the stack.

The next symbol is ‘/’. ‘/’ has lower precedence than ‘d’. So, pop out ‘d’ and append it in postfix.

Postfix: a b c * + d

Now, the stack has only one symbol, which is ‘-‘. ‘/’ has higher precedence, so we’ll push ‘/’ into the stack.

The last symbol of the expression is ‘e’. ‘e’ has higher precedence than ‘/’. So push ‘e’ into the stack.

Now that we have reached the end of the expression, no symbols remain. So, we’ll remove all the elements or symbols from the stack and append them to the postfix.

Postfix: a b c * + d e / –

This is the final postfix expression.

Steps to Perform the Conversion of Infix to Postfix:

Step 1: If the stack is empty, push the first symbol (operand or operator) into the stack.

Step 2: Two conditions,

• If the symbol (operator or operand) present in the stack has lower precedence than the current symbol of expression, push that symbol into the stack.
• If the symbol (operator or operand) present in the stack has higher precedence than the current symbol of expression, pop out the symbol from the stack and append that in the postfix.

After popping out, if any symbol is present in the stack, check again for the above two conditions and take action accordingly. If the stack is empty, push that element.

Step 3: If you have reached the end of the expression and the stack is not empty, remove all the symbols from the stack and write them in Postfix.

So, we have seen two methods of conversion of infix to postfix. In the first method, only operators are pushed into the stack, and in the second method, operators and operands are pushed into the stack.

Note: In this method, the condition is that the operands must have higher precedence.

In the next article, I will discuss Program for Infix to Postfix Conversion in C Language. Here, in this article, I explain Infix to Postfix using Stack in C Language with Examples. I hope you enjoy this article on Infix to Postfix using Stack in C.