Associativity and Unary Operators in C

Back to: Data Structures and Algorithms Tutorials

Associativity and Unary Operators in C:

In this article, I will discuss Associativity and Unary Operators in C with Examples. Please read our previous article discussing Infix to Postfix Conversion in C. We’ll explore how to handle unary operators when converting infix to prefix or postfix. So, let’s delve into what associativity entails.

What is Associativity?

To understand associativity, we have selected a few operators.

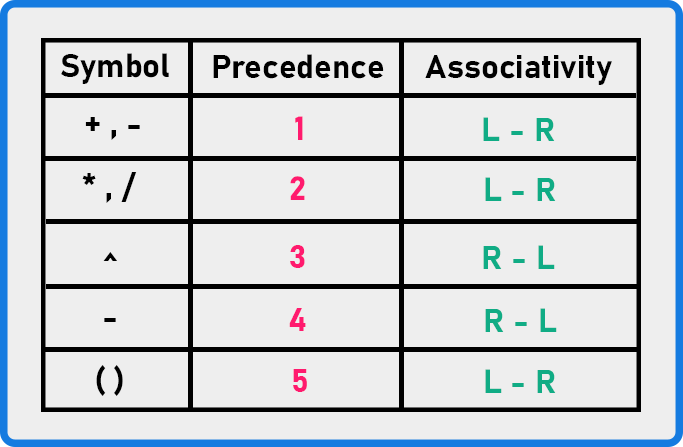
In our previous article, we utilized +, -, *, and / operators. We’ve now introduced ^ (power operation) and – (unary minus). In terms of precedence, the power operation has a precedence of 3, while unary minus has a precedence of 4, which is higher than +, -, *, and /. Brackets have the highest precedence.

If you examine the associativity in the above table, three operations (+, -, *, /, ()) have left-to-right associativity, while two operations (^ and unary minus) have right-to-left associativity. Let’s delve into the discussion about associativity.

In the previous article, we explained that precedence and associativity are essential for the parenthesization of an expression. If we don’t explicitly parenthesize expressions in our program, the compiler will logically parenthesize them based on this precedence and associativity table.

This is an expression with multiple operators having the same precedence. According to the associativity, which is left to right, we should select them from left to right. If this expression is properly parenthesized, it will look like:

So, the order of operations is:

Let’s consider one more example.

We can write this type of expression in our C/C++ programs. It means “a” is assigned with “b”, “b” is assigned with “c”, and “c” is assigned with 5. So, first, 5 is assigned to “c”, then to “b”, and finally to “a”. You can observe that it is working from right to left. Again, there are multiple operators with the same precedence. So, which one should we take first? Its associativity is from right to left. We will parenthesize this expression based on the associativity because the precedence is the same here.

Parenthesization is performed from right to left. Therefore, from these two examples, we can understand that there are two types of associativities: left-to-right and right-to-left.

So, if the precedences are equal, then we look at associativity. Now, let us show you the postfix notation for these expressions.

Infix to Postfix Conversion:

Let’s convert the first expression: (((a + b) + c) – d).

First, convert (a + b),

=> (([a b +] + c) – d).

Here, we convert [a b +] + c,

=> ([a b + c +] – d)

=> a b + c + d –

This is the postfix form of the first expression.

Now, let’s convert the next expression: (a = (b = (c = 5))).

First, c = 5 will be converted,

=> (a = (b = [c 5 =]))

Now, b = [c 5 =] will be converted,

=> (a = [b c 5 = =])

=> a b c 5 = = =

This is the postfix form of the second expression. Indeed, postfix notation depends on the parenthesization, and the parentheses are influenced by precedence and associativity. Let’s examine a few more examples based on right-to-left associativity operators. We’ll introduce some operators that are not even in the above table.

Example based on Right to Left Associativity:

Example 1: a ^ b ^ c

This expression involves two power operations, which serves as a good example of right-to-left associativity. ‘^’ is represented by a caret symbol. Some authors may use a dollar symbol instead, but we’re using the caret symbol here. Power operations are right-to-left associative. Therefore, if there are multiple operators in the same expression with the same precedence, it should be parenthesized from right to left.

=> (a ^ (b ^ c))

Now, it is parenthesized. Let’s convert this into postfix form.

So, first (b ^ c) will be converted,

=> (a ^ [b c ^])

Now, the remaining operator will be converted,

=> a b c ^ ^

This is the postfix form of the above expression.

Note:

Let’s look at the above expression mathematically. It means that c is a power of b, i.e., b^c, and b^c is a power of a. Mathematically, the expression (a ^ (b ^ c)) with right-to-left associativity will look like this:

If you want to try it from left to right associativity, b is a power of a i.e. a^b and a^b is a power of c. It will look like,

It is wrong. As we all know, the power operator has right-to-left associativity. The caps operator is not present in the C/C++ language, but it used to be present in previous or older languages.

Examples based on Unary Operator:

Let us take some unary operator and convert them into prefix and postfix.

Example 2: -a

This is the negation of a. This expression involves unary minus. Unary minus has a precedence of 4, which is the highest among all the operators we’ve seen above, except for brackets. It has right-to-left associativity. If we have more than one unary minus in an expression, we start from left to right. Let’s write the prefix notation of −a.

Prefix: -a

The expression will remain the same in prefix notation.

Postfix: a-

The operand will be written first, followed by the operator in postfix form.

Example 3: – – a

In this expression, we should put the rightmost minus in the bracket first as we evaluate from right to left.

( – ( – a))

In this way, both minuses will be enclosed in brackets. So, first, the right-hand side minus will be taken, and then the left-hand side. The postfix and prefix forms are:

Prefix: – – a

Postfix: a – –

Example 4: *p

As you all know, ‘*’ is a dereferencing operator in the C/C++ language. It is used to access the data wherever the pointer is pointing. This is the regular or infix form.

Prefix: *p

The prefix form is also the same as the infix form because it is a unary operation, not a binary operation.

Postfix: p*

If there are multiple operators, like **p, then the rightmost operator will be evaluated first. They will be parenthesized from right to left.

( * ( * p))

This is how parenthesization will be done for **p.

Example 5: n!

Prefix and postfix form of n factorial are,

Prefix: !n

Postfix: n!

Postfix is the same as regular form or infix form.

Example 6: log x

The prefix will be same as infix.

Prefix: log x

Postfix: x log

As operators come afterward in postfix notation, we have to write “log” after “x”. In prefix notation, the operator comes before the operand, so “log” is already written before “x”. We’ve shown you a few examples of unary operators. In programming languages, unary operators have higher precedence and right-to-left associativity. Now, let’s take a complex expression with different operators and convert it into postfix notation.

Example 7: – a + b * log n!

Let’s convert this into a postfix according to the precedence and associativity of operators. In this expression, which operator has higher precedence? Unary operators. How many unary operators are there? Three unary operators: -, log, and ! (factorial). They all have the same precedence, and the associativity is right to left. So, which operator will be converted first? The Factorial will be converted first.

=> – a + b * log [n!]

The postfix of n! is same. So, no changes have been made to this operation. Now, the log will be converted.

=> – a + b * [n! log]

Here, n! is written before the log. Now, next is the unary minus.

=> [a -] + b * [n! log]

We have converted all the unary operators. Addition and multiplication are remaining. So which one has higher precedence? Multiplication.

=> [a -] + [b n! log *]

Now, the only addition is remaining.

=> a – b n! log * +

So, this is the postfix form of the [- a + b * log n!] expression.

We have highlighted the operations that we have performed step by step. You can understand the process and practice more examples on your own. That’s all about associativity and unary operators.

In the next article, I will discuss Infix to Postfix using Stack in C. Here, in this article, I explain Associativity and Unary Operators in C Language with Examples. I hope you enjoy this Associativity and Unary Operators in C article.