Height vs Nodes in a Binary Tree

Back to: Data Structures and Algorithms Tutorials

Height vs Nodes in Binary Tree:

In this article, we will explore the formulas for calculating the height and the number of nodes in a Binary Tree. Please read our previous article discussing the basis of Binary Tree Data Structure.

What are the Height and Node Formulas of a Binary Tree?

If we know the height of a binary tree, we can calculate the minimum and maximum number of nodes. Similarly, if the number of nodes is given, we can calculate the maximum and minimum height of the binary tree. Let’s first learn how to calculate the maximum and minimum number of nodes when the height of a binary tree is given.

How Do We Calculate the Maximum and Minimum Number of Nodes if the Height of a Binary Tree is Given?

Let us take an example.

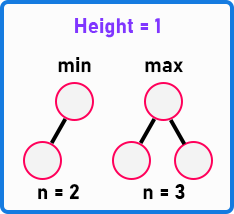
Here, the height of a binary tree is given as 1. We all know that height starts from 0. When the height of a binary tree is 1, how many nodes are required at a minimum? The answer is two nodes. If we remove any node from these two nodes, the tree will have a height of 0, not 1. So, a minimum of 2 nodes is needed to make a tree of height 1.

How many nodes are required at a maximum for a binary tree of height 1? You can see in the above diagram that three nodes are required. Let us take another example.

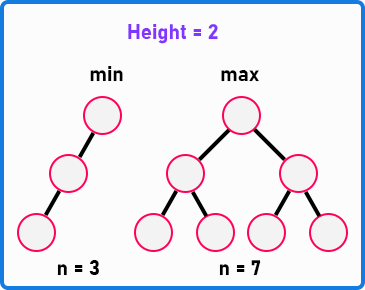
In this example, the height of the binary tree is 2, i.e., 0, 1, and 2. So, what are the minimum and maximum numbers of nodes required for a binary tree of height 2? The minimum is three nodes, and the maximum is seven nodes.

If the height of the binary tree is 3, i.e., 0, 1, 2, and 3, what are the minimum and maximum numbers of nodes required in this case? The minimum is four nodes, and the maximum is 15 nodes.

Formula for the Minimum Number of Nodes in a Binary Tree:

We have seen three examples, and now we can generate the formula based on observation. Let’s first check the minimum number of nodes.

• If height = 1, then the minimum number of nodes = 2
• If height = 2, then the minimum number of nodes = 3
• If height = 3, then the minimum number of nodes = 4

To get the minimum number of nodes, we add 1 to the height. Therefore, the formula to calculate the minimum number of nodes is: n = h + 1

Formula for the Maximum Number of Nodes in a Binary Tree:

Now, let’s calculate the formula for the maximum number of nodes.

• If height = 1, then the maximum number of nodes = 3
• If height = 2, then the maximum number of nodes = 7
• If height = 3, then the maximum number of nodes = 15.

We cannot easily observe a pattern here. Let’s consider the binary tree with the maximum number of nodes for a height of 3.

In the diagram above, the number of nodes is written for each tree level. Level 1 has one node, Level 2 has two nodes, Level 3 has 2² nodes, and Level 4 has 2³ nodes. So, the total number of nodes will be

Total no. of nodes = 1 + 2 + 2² + 2³ = 15

Is there a formula for this sequence? Yes, it is a Geometric Progression (GP) series.

GP Series = a + ar + ar² + ar³ + … + ar^k = a (r^k+1 – 1) / (r -1)

Here, “a” is the first term, and “r” is the common ratio. The formula for this series is:

a (r^k-1 – 1) / (r -1).

The extended version for 1 + 2 + 2² + 2³ series is,

1 + 2 + 2² + 2³ + … + 2^h

Here, a = 1 (the first term) and r = 2 (divide any term by the previous term to get the ratio). Let’s put the values a and r into the formula.

1 + 2 + 2² + 2³ + … + 2^h = 1 (2^h+1 – 1) / (2 -1)

= 2^h+1 – 1

So, the sum of the terms 1, 2, 2², 2³, …, 2^h will equal 2^h+1 – 1. Let’s come back to our example. As we have the expression 1 + 2 + 2² + 2³. Let’s calculate the value of this expression with the formula, where h = 3.

= 2^h+1 – 1

= 2³⁺¹ – 1

= 2⁴ – 1

= 16 – 1 = 15

= 2^h+1 – 1

We got the correct answer. So, now, we can calculate the maximum number of nodes in a binary tree. Following are the formulas,

Formula for Minimum number of nodes: n = h + 1

Formula for Maximum number of nodes: n = 2^h+1 – 1

We have the formulas to calculate the max and min number of nodes if height of the binary tree is given. Now, if a number of nodes is given, we want to calculate the minimum and maximum height of the binary tree.

How Do We Calculate the Maximum and Minimum Height of a Binary Tree if the Number of Nodes is Given?

Let’s take an example.

In this example, we have three nodes. Using three nodes, we can generate a binary tree with a minimum height of 1. We can stretch the tree and generate a binary tree with a maximum height of 2.

With 7 nodes, we can generate a binary tree with a minimum height of 2 and a maximum height of 6.

In this example, we have 15 nodes. We can generate a binary tree with a minimum height of 3. The 15 nodes can be stretched in the left, right, or left-right directions so that a binary tree can be generated with a maximum height of 14. Let’s discover the formula for the maximum height.

Formula for the Maximum Height of a Binary Tree:

From the above three examples, we observed a pattern in the maximum height of a binary tree:

• If the number of nodes = 3, then the maximum height of the binary tree = 2
• If the number of nodes = 7, then the maximum height of the binary tree = 6
• If the number of nodes = 15, then the maximum height of the binary tree = 14

So, the maximum height will always be one less than the total number of nodes, i.e., 2 (3 -1), 6 (7 -1), 14 (15 – 1). We derived the formula for the maximum height:

Max height of a binary tree = Total number of nodes – 1

h = n – 1

Formula for the Minimum Height of a Binary Tree:

Here, we will try to find some relation between the minimum height and the number of nodes:

• If the number of nodes = 3, then the minimum height of the binary tree = 1
• If the number of nodes = 7, then the minimum height of the binary tree = 2
• If the number of nodes = 15, then the minimum height of the binary tree = 3

We are unable to find a pattern in this case. However, we can derive the formula for the minimum height with the help of the number of nodes formula:

Formula for Minimum number of nodes: n = h + 1

Formula for Maximum number of nodes: n = 2^h+1 – 1

We derived these two formulas to find the maximum and minimum number of nodes in a binary tree if the height of the binary tree is given. Now, we want to derive the formulas to find a binary tree’s maximum and minimum height if the number of nodes is given. We already derived the formula for the maximum height, but you can also get that formula with the help of the minimum number of nodes formula, which is:

n = h + 1

h = n – 1

So, the minimum number of nodes formula gives the maximum height formula. We can use the maximum number of nodes formula to derive the minimum height formula. So, we don’t need to observe the examples; we can directly derive the formula. Let’s convert the maximum number of nodes formula to the minimum height formula:

n = 2^h+1 – 1

n + 1 = 2^h+1

2^h+1 = n + 1 (just changed the side)

h + 1 = log₂ (n + 1) (convert the left-hand side power into the log in the left-hand side)

h = log₂ (n + 1) – 1

So, here we have the formula for the minimum height of a binary tree when the number of nodes is given:

Minimum height of binary tree = log₂ (number of nodes + 1) – 1

h = log₂ (n + 1) – 1

Let us verify this formula. We have 15 total nodes, so the minimum height should be 3. Let’s check the minimum height of the binary tree with this formula:

h = log₂ (n + 1) – 1

h = log₂ (15 + 1) – 1

h = log₂ (16) – 1

h = 4 – 1 (log₂ (16) = 4)

h = 3

This is the correct answer.

So, the conclusion is that if you know the height formula, you can derive the formula for nodes and vice versa. So, if the total no. of nodes is given,

Formula for Minimum height: h = log₂ (n + 1) – 1

Formula for Maximum height: h = n – 1

Range of Values for Number of Nodes and Height of a Binary Tree:

Finally, from the observation, we got the range of values.

Number of Nodes in a Binary Tree:  h + 1 <= n <= 2^{h + 1} – 1

This is the formula for a number of nodes in a binary tree.

Minimum Nodes: h + 1

Maximum Nodes: 2^{h + 1} – 1

This formula is based on the height. If you know the height of a binary tree, then you can calculate the maximum and minimum number of nodes in it.

Height of Binary Tree:

log₂ (n + 1) – 1 <= h <= n – 1

This is the formula for calculating the maximum and minimum height of a binary tree. It ranges from logarithmic to linear. The minimum is O (log n), and the Maximum is O (n).

Minimum Nodes: log₂ (n + 1) – 1

Maximum Nodes: n – 1

In the next article, I will discuss Internal vs. External Nodes in a Binary Tree with Examples. In this article, I explain height vs nodes in a binary tree using C language with examples. I hope you enjoy the Height vs. Nodes in a Binary Tree article.