Back to: C#.NET Programs and Algorithms
Fibonacci Series Program in C# with Examples
In this article, I am going to discuss the Fibonacci Series Program in C# with Examples. This is one of the most frequently asked C# written interview questions. Please read our previous article where we discussed the Swapping Program with and without using the third variable in C#. As part of this article, we are going to discuss the following pointers.
- What is the Fibonacci Series?
- What are the different ways to implement the Fibonacci in C#?
- How to find the nth Fibonacci number in C#?
- How to Print the Fibonacci Series up to a given number in C#?
What is the Fibonacci Series?
The Fibonacci series is nothing but a sequence of numbers in the following order:
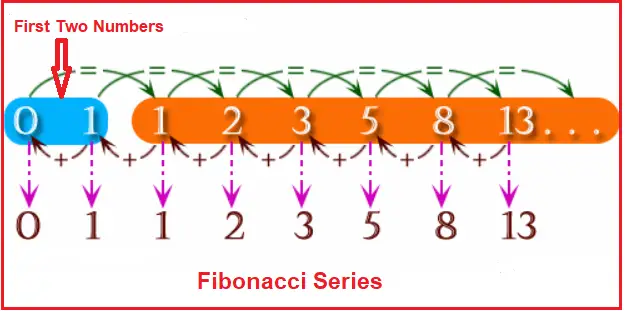
The numbers in this series are going to start with 0 and 1. The next number is the sum of the previous two numbers. The formula for calculating the Fibonacci Series is as follows:
F(n) = F(n-1) + F(n-2) where:
F(n) is the term number.
F(n-1) is the previous term (n-1).
F(n-2) is the term before that (n-2).
What are the different ways to implement the Fibonacci in C#?
In C#, we can print the Fibonacci Series in two ways. They are as follows:
- Iterative Approach
- Recursion Approach
Iterative Approach to Print Fibonacci Series in C#:
This is the simplest approach and it will print the Fibonacci series by using the length. The following program shows how to use the iterative approach to print the Fibonacci Series in C#.
using System;
namespace LogicalPrograms
{
public class Program
{
public static void Main()
{
int firstNumber = 0, SecondNumber = 1, nextNumber, numberOfElements;
Console.Write("Enter the number of elements to Print : ");
numberOfElements = int.Parse(Console.ReadLine());
if(numberOfElements < 2)
{
Console.Write("Please Enter a number greater than two");
}
else
{
//First print first and second number
Console.Write(firstNumber + " " + SecondNumber + " ");
//Starts the loop from 2 because 0 and 1 are already printed
for(int i = 2; i < numberOfElements; i++)
{
nextNumber = firstNumber + SecondNumber;
Console.Write(nextNumber + " ");
firstNumber = SecondNumber;
SecondNumber = nextNumber;
}
}
Console.ReadKey();
}
}
}
Output:

Recursive Approach to Print Fibonacci Series in C#:
In the Recursive Approach, we need to pass the length of the Fibonacci Series to the recursive method and then it will iterate continuously until it reaches the goal. Let us understand this with an example.
using System;
namespace LogicalPrograms
{
public class Program
{
static void Main(string[] args)
{
Console.Write("Please enter the Length of the Fibonacci Series : ");
int number = int.Parse(Console.ReadLine());
FibonacciSeries(0, 1, 1, number);
Console.ReadKey();
}
public static void FibonacciSeries(int firstNumber, int secondNumber, int counter, int number)
{
Console.Write(firstNumber + " ");
if (counter < number)
{
FibonacciSeries(secondNumber, firstNumber + secondNumber, counter + 1, number);
}
}
}
}
Output:

How to find the nth Fibonacci number in the Fibonacci Series in C#?
It is also possible to print the nth Fibonacci number from the Fibonacci series in C#. The following example prints the nth number from the Fibonacci series.
Using Recursion:
using System;
namespace LogicalPrograms
{
public class Program
{
static void Main(string[] args)
{
Console.Write("Please enter the Nth number of the Fibonacci Series : ");
int NthNumber = int.Parse(Console.ReadLine());
//Decrement the Nth Number by 1. This is because the series starts with 0
NthNumber = NthNumber - 1;
Console.Write(NthFibonacciNumber(NthNumber));
Console.ReadKey();
}
private static int NthFibonacciNumber(int number)
{
if ((number == 0) || (number == 1))
{
return number;
}
else
{
return (NthFibonacciNumber(number - 1) + NthFibonacciNumber(number - 2));
}
}
}
}
Output:

You can observe that, in the above implementation, it does a lot of repeated work. So this is a bad implementation to find the nth Fibonacci number in the Fibonacci series. We can avoid this using the iterative approach.
Without Using Recursive Function:
Let us understand how to implement this with an example. Here we are not going to use the Recursive function.
using System;
namespace LogicalPrograms
{
public class Program
{
static void Main(string[] args)
{
Console.Write("Please enter the Nth number of the Fibonacci Series : ");
int NthNumber = int.Parse(Console.ReadLine());
//Decrement the Nth Number by 1. This is because the series starts with 0
NthNumber = NthNumber - 1;
Console.Write(NthFibonacciNumber(NthNumber));
Console.ReadKey();
}
private static int NthFibonacciNumber(int number)
{
int firstNumber = 0, secondNumber = 1, nextNumber = 0;
// To return the first Fibonacci number
if (number == 0)
return firstNumber;
for (int i = 2; i <= number; i++)
{
nextNumber = firstNumber + secondNumber;
firstNumber = secondNumber;
secondNumber = nextNumber;
}
return secondNumber;
}
}
}
Output:
![]()
How to Print the Fibonacci Series up to a given number in C#?
Now we will see how to print the Fibonacci up to a given number in C#. Please have a look at the following program.
using System;
namespace LogicalPrograms
{
public class Program
{
static void Main(string[] args)
{
int firstNumber = 0, SecondNumber = 1, nextNumber, number;
Console.Write("Enter the number upto which print the Fibonacci series : ");
number = int.Parse(Console.ReadLine());
//First print first and second number
Console.Write(firstNumber + " " + SecondNumber + " ");
nextNumber = firstNumber + SecondNumber;
//Starts the loop from 2 because 0 and 1 are already printed
for (int i = 2; nextNumber < number; i++)
{
Console.Write(nextNumber + " ");
firstNumber = SecondNumber;
SecondNumber = nextNumber;
nextNumber = firstNumber + SecondNumber;
}
Console.ReadKey();
}
}
}
Output:
![]()
Here, in this article, I try to explain the Fibonacci Program Program in C# with Examples. I hope you enjoy this article. In the next article, I am going to discuss the Prime Number Program in C# with some examples.
